Problemstellung:
Für 32Bit und 64Bit Office Versionen
In einem 100m Rennen treten 8 Läufer an.
Es geht um Gold, Silber und Bronze.
Wieviele Möglichkeiten der Belegung der Plätze 1-3 gibt es?
Voraussetzungen:
Das Bsp ist ab A00 lauffähig.
Lösung:
Zuerst benötigen wir gesamte Anzahl der Möglichkeiten.
Die Fakultät (math. Zeichen !) ist das Produkt der natürlichen Zahlen von 1 bis n definiert.
Es sind nur positive Ganzzahlen möglich. Werte über 170 können mit VB(A) nicht berechnet werden.
Mathematische Formel:
Zuerst benötigen wir gesamte Anzahl der Möglichkeiten.
Die Fakultät (math. Zeichen !) ist das Produkt der natürlichen Zahlen von 1 bis n definiert.
Es sind nur positive Ganzzahlen möglich. Werte über 170 können mit VB(A) nicht berechnet werden.
Mathematische Formel:
n!=1*2*3*4*...*n
In VBA gibt es zur Berechnung mehrere Lösungen, hier nur eine Möglichkeit
Public Function Fakultaet(ByVal intN As Integer) As Variant Dim dblFakultaet As Double Dim lngZaehler As Long On Error Resume Next dblFakultaet = 1 For lngZaehler = 1 To intN dblFakultaet = dblFakultaet * lngZaehler Next lngZaehler If Err = False Then Fakultaet = dblFakultaet Else Fakultaet = "Fehler!" Err.Clear End If On Error GoTo 0 End Function
Für unser Bsp. ergäbe das also:
1*2*3*4*5*6*7*8=40320
Möglichkeiten
1*2*3*4*5*6*7*8=40320
Möglichkeiten
Jetzt wollten wir aber nur die Anzahl der Möglichkeiten haben mit denen die Plätze 1-3 belegt werden können.
Hier kommt dann die Variation zum Einsatz.
Mathematische Formel:
x=n!/(n-k)!
In VBA:
Public Function Variation(iAllElements As Integer, iSelectElements As Integer) As Long Dim nFakultaet As Long Dim nElemente As Long nFakultaet = Fakultaet(iAllElements) nElemente = Fakultaet(iAllElements - iSelectElements) Variation = nFakultaet / nElemente End Function
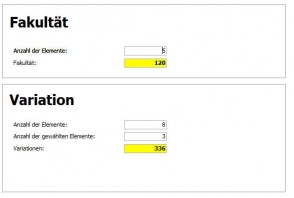
Für unser Bsp: x=40230/120=336
Also ergeben sich 336 Möglichkeiten bei 8 Läufern wie die Plazierung der Plätze 1-3 belegt sein können.
Jetzt möchte wir aber auch noch die Namen der Plazierten haben.
Somit kommen wir nun zur Permutation.
Den Code könnt Ihr der Bsp-DB entnehmen.
Der Aufruf sähe dann so aus:
Private Sub cmd_CreatePermut_Click() Dim i As Long, j As Long, k As Long Dim TmpSArray() As String Dim sTmp As String, sResult As String Me.Text1 = Null If Me.txt_Tiefe = 0 Or IsNull(Me.txt_Tiefe) Then Me.txt_Tiefe = 3 txt_CountVari = Variation(8, Me.txt_Tiefe) For i = 1 To Me.txt_Tiefe sTmp = PermutateString(1, i, "Beier|Büttner|Heinze|Kunze|Müller|Schmidt|Mayer|Dietze") Next i TmpSArray = Split(sTmp, "|", , vbTextCompare) k = 0 For j = LBound(TmpSArray) To UBound(TmpSArray) If TmpSArray(j) <> "" Then k = k + 1 sResult = sResult & "[" & k & "] " & TmpSArray(j) & vbNewLine End If Next j Me.Text1 = sResult End Sub
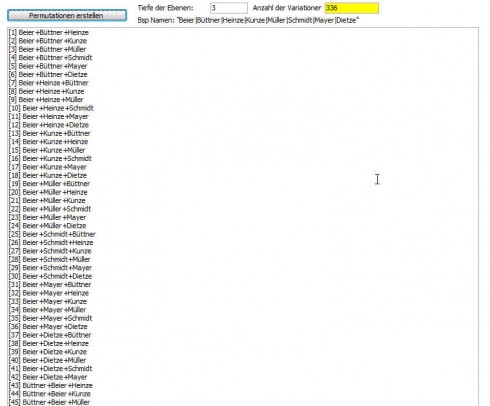
Wir über geben der Funktion in diesem Fall die Anzahl der Plätze die wir haben wollen in unserem Fall=3
und die Namen="Beier|Büttner|Heinze|Kunze|Müller|Schmidt|Mayer|Dietze"
Als Trennzeichen bitte das Pipesymbol (|) verwenden.
Der Aufruf erstellt uns eine Liste mit den 336 Möglichkeiten der Belegung der Plätze 1-3
Dateien:
Für 32Bit und 64Bit Office Versionen
Arbeiten mit Fakultät, Variationen und Permutationen
ab A00
Die Zip-Datei enthält eine Version ab A00
Ähnliche Artikel





Weiterlesen...